처음부터 차근차근
좋은 수 구하기 본문
반응형
문제(제한 시간 : 2초)
https://www.acmicpc.net/problem/1253
1253번: 좋다
첫째 줄에는 수의 개수 N(1 ≤ N ≤ 2,000), 두 번째 줄에는 i번째 수를 나타내는 Ai가 N개 주어진다. (|Ai| ≤ 1,000,000,000, Ai는 정수)
www.acmicpc.net
문제를 해석해보자면
여기서 말하는 좋은 수란 두 번째 줄에 주어진 수 중 5로 예를 들어보자.
5는 두 번째 줄에 있는 수 중에 2 + 3이라는 조합으로 만들 수 있는 수이다.
그래서 5를 좋은 수라고 한다.
두 번째 줄에 있는 수 중 좋은 수의 개수를 구하는 것이 이 문제의 목표이다.
문제 풀이
이 문제는 투포인터 알고리즘을 사용해야한다.
투포인터 알고리즘을 사용해서 양 쪽 끝에서부터 가운데로 오면서 만나는 숫자를 합하여 좋은 수인지 판별한다.
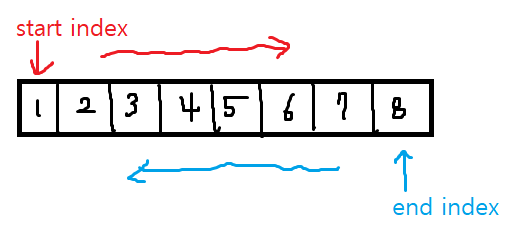
여기서 주의해야할 점이 좋은 수를 찾는 계산을 할 때 자기 자신이 포함되지 않아야 한다는 점이다.
문제에
두 번째 줄에는 i번째 수를 나타내는 Ai가 N개 주어진다. (|Ai| ≤ 1,000,000,000, Ai는 정수)
라고 쓰여져 있는 걸 보면 두 번 째 줄에 들어가는 수들이 0이어도 된다는 소리이다.
즉, 계산할 때 자기 자신을 포함하는 경우가 생긴다는 것인데 그래서 이 경우를 제외시켜줘야한다.
그래서 if 문을 통해 좋은 수를 골라도 자기 자신이 합으로 들어간 조합이 아닌지 다시 한 번 더 확인해야한다.
내 풀이
import java.io.*;
import java.util.*;
public class Main
{
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int num = Integer.parseInt(br.readLine());
int[] arr = new int[num];
int result = 0;
StringTokenizer st = new StringTokenizer(br.readLine());
for (int i = 0; i < num; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
Arrays.sort(arr); // 배열 오름차순 정렬
for (int i = 0; i < num; i++) {
int find = arr[i];
int start_index = 0;
int end_index = num - 1;
while (start_index < end_index) {
if (find < arr[start_index] + arr[end_index]) {
end_index--;
}
else if (find == arr[start_index] + arr[end_index]) {
if (i != start_index && i != end_index) { // 자기자신을 포함하지 않은 경우
result++;
break;
}
else if (i == start_index) { // 자기자신을 포함한 경우
start_index++;
}
else if (i == end_index) { // 자기자신을 포함한 경우
end_index--;
}
}
else if (find > arr[start_index] + arr[end_index]) {
start_index++;
}
}
}
bw.write(String.valueOf(result));
bw.flush();
br.close();
bw.close();
}
}
참고 : do it 알고리즘 코딩테스트 자바편
반응형
'알고리즘' 카테고리의 다른 글
| 그리디 알고리즘 (0) | 2022.10.13 |
|---|---|
| DFS, BFS 알고리즘 (0) | 2022.10.10 |
| 구간 합 구하기 (0) | 2022.10.07 |
| 평균 구하기 (0) | 2022.09.27 |
| 평균 넘는 사람 비율 구하기 (0) | 2022.09.24 |
Comments


